Binomial distribution

binomial
Probability mass function
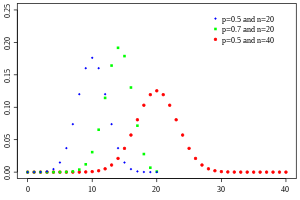
Cumulative distribution function
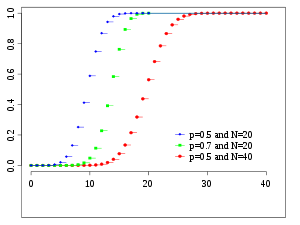
Notation	B(n, p)
Parameters	n ∈ N₀ — number of trials p ∈ [0,1] — success probability in each trial
	k ∈ { 0, …, n } — number of successes
pmf	$\textstyle {n \choose k}\,p^{k}(1-p)^{n-k}$ $\textstyle {n \choose k}\,p^{k}(1-p)^{n-k}$
CDF	$\textstyle I_{1-p}(n-k,1+k)$ $\textstyle I_{1-p}(n-k,1+k)$
Mean	$np$ $np$
Median	$\lfloor np\rfloor$ $\lfloor np\rfloor$ or $\lceil np\rceil$ $\lceil np\rceil$
	$\lfloor (n+1)p\rfloor$ $\lfloor (n+1)p\rfloor$ or $\lceil (n+1)p\rceil -1$ $\lceil (n+1)p\rceil -1$
Variance	$np(1-p)$ $np(1-p)$
Skewness	${\frac {1-2p}{\sqrt {np(1-p)}}}$ ${\frac {1-2p}{\sqrt {np(1-p)}}}$
Ex. kurtosis	${\frac {1-6p(1-p)}{np(1-p)}}$ ${\frac {1-6p(1-p)}{np(1-p)}}$
Entropy	${\frac {1}{2}}\log _{2}{\big (}2\pi e\,np(1-p){\big )}+O\left({\frac {1}{n}}\right)$ ${\frac {1}{2}}\log _{2}{\big (}2\pi e\,np(1-p){\big )}+O\left({\frac {1}{n}}\right)$ in . For , use the natural log in the log.
MGF	$(1-p+pe^{t})^{n}\!$ $(1-p+pe^{t})^{n}\!$
	$(1-p+pe^{it})^{n}\!$ $(1-p+pe^{it})^{n}\!$
PGF	$G(z)=\left[(1-p)+pz\right]^{n}.$ $G(z)=\left[(1-p)+pz\right]^{n}.$
Fisher information	$g_{n}(p)={\frac {n}{p(1-p)}}$ $g_{n}(p)={\frac {n}{p(1-p)}}$ (for fixed $n$ $n$ )

$g_{n}(p)={\frac {n}{p(1-p)}}$ $g_{n}(p)={\frac {n}{p(1-p)}}$

In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent yes/no experiments, each of which yields success with probability p. A success/failure experiment is also called a Bernoulli experiment or Bernoulli trial; when n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.

The binomial distribution is frequently used to model the number of successes in a sample of size n drawn from a population of size N. If the sampling is carried out without replacement, the draws are not independent and so the resulting distribution is a hypergeometric distribution, not a binomial one. However, for N much larger than n, the binomial distribution remains a good approximation, and widely used.

In general, if the random variable X follows the binomial distribution with parameters n ∈ ℕ and p ∈ [0,1], we write X ~ B(n, p). The probability of getting exactly k successes in n trials is given by the probability mass function:

...
Wikipedia